Context

Research Paper: https://users.soe.ucsc.edu/~pkouki/kouki-recsys19.pdf

Year: 2019

Models: Siamese Neural Networks & BiLSTM

Topic: 2-Stage Recommender System (Candidate Generator + Ranker)

Keywords: #Embeddings #Item-to-item #Multimodal #Online-recommender-system

Introduction

In this first article, we will study the method proposed by Home Depot to recommend products on each product page. The recommender system proposed in this research paper is characterized as Item-to-item. This means that the data used to build the system is primarily derived from the products. We are dealing with a non-personalized recommendation engine.

The goal of this engine is to propose a set of products, referred to as collections, that are related to the product page the user is currently viewing. These suggestions can be presented in sections like “Similar Products” or “Complementary Products.”

The approach proposed by Home Depot is a classic one in the field of recommender systems. It is divided into two phases:

1. Generating a set of candidate products (or CG).
2. Ranking these candidates.

Before diving into the details of the methods used, let’s review a few definitions.

1. A Few Definitions

• $P$ = Set of products.

$$ P = {p_1,…,p_k} $$

• $A_i$ = Set of attributes for product $p_i$. Attributes include title, description, brand, color, etc.

$$ A_i = {a_{i,1},…,a_{i,l}} $$

• $C$ = Set of categories

$$ C = {c_1,…,c_k} $$

• $R$ = Set of relationships between categories. For example: $r(Ci,Cj)$ means that $C_j$ is a subcategory (shared subclass relationship) of $C_i$.

$$ R = {r(Ci,Cj), ∀Ci,Cj ∈ C,i < j}. $$

• $h$ = A hierarchy represents a set of ordered categories linked by subclass relationships.

$$ h = (C1,C2, …,Ck−1,Ck) ~where~r(Ci,Ci+1) ∈ R, i = 1…k $$ $$ H ~is~the~set~of~all~possible~hierarchies. $$

• The problem formulation is as follows:

$$ For~ a ~product~p_a~ we~want~a~set~of~products~Pc = {p_{c,1}, …,p_{c,k}} $$ $$ such~that:~{p_a,p_{c,1},…,p_{c,k}}~with~the~following~hierarchies~Hc ={h_a,h_{c,1}, …,h_{c,k}} $$ $$ are~relevant~to~the~user $$

In general, business rules are used to enforce such constraints. In this research paper, the answer to this problem is as follows:

(1) = The color of the products must be the same, and the title as well as the description must be similar.

$$ (1) ~ ∀p_i ∈ Pc : color_{pi} = color_{pa}, ~ title_{pi} ≈ title_{pa}, ~ description_{pi} ≈ description_{pa} $$

(2) = The entire collection of products must share the same root category among themselves and also have the same root category as the “Anchor” product.

$$ (2) ~ ∀h_i,h_j ∈ H_c : C_{i,1} = C_{j,1} $$

(3) = The set of hierarchies to which the collection products belong, \H_c\, cannot contain duplicates. The idea is to avoid proposing interchangeable products.

$$ ∀h_i,hj ∈ H_c : h_i \neq h_j $$

Now that all the definitions are established, we can move on to calculating the score for generating a set of candidate products for the collection.

2. Candidate Generation

Two methods are proposed in the research paper.

1. Using domain knowledge (Candidate Generator 1 - CG 1)

At this stage, we will establish a link between categories.

The process begins by retrieving all products provided by domain experts denoted $P_m$. For each product, denoted $p_{m_i}$ and part of $P_m$, we identify the hierarchy assigned to it, denoted $h_i$.

Then, each relationship between products, denoted $r_m(p_{m_i}, p_{m_j})$ and belonging to $R_m$, is transformed into a relationship between their respective hierarchies. This transformation yields $Q_m = {q_m(h_i,h_j),…,q_m(h_k,h_l)}$ where $p_{m,i}$ and $p_{m,j}$ are associated with hierarchies $h_i$ and $h_j$ respectively.

This process generates a set of relationships between hierarchies, denoted $Q_m$. Within this set, the same relationship can appear multiple times.

After this step, we calculate the co-occurrence probability for each pair of hierarchies $(h_i,h_j)$. This probability, denoted $Prob_m(h_i,h_j) = \frac{N(q_{m}(h_i,h_j))}{N(h_i)}$ , is calculated by dividing the frequency of the pair $(h_i,h_j)$ in $Q_m$ by the frequency of the hierarchy $h_i$ in $Q_m$.

It is essential to note that this probability calculation is performed only for pairs of hierarchies with the same root category.

Here is a concrete example:

1. Product Collection: Suppose interior design experts provide us with a list of products for the kitchen and bathroom, such as pans, spatulas, towels, faucets, sponges, soaps, etc. This list is our $P_m$. We repeat this step for each expert domain. Here, “Kitchen” and “Bathroom”.

2. Product Hierarchy: Each product belongs to a specific category:

   • Kitchen Utensils: pans, spatulas
   • Small Appliances: blender, mixer
   • Bathroom Accessories: towels, soaps
   • Bathroom Fixtures: faucets
   • Cleaning Products: sponges

3. Relationships Between Products: Suppose, based on the data provided by the experts, we determine that:

   • The spatula and the pan are related because they appear together in several provided collections.
   • Similarly, the spatula is linked to small appliances because they are found together in some collections, such as those from the same brand or in an equipped kitchen.
   • Towels and soaps are also related for similar reasons.

   These relationships are our $R_m$.

4. Transformation into Hierarchy Relationships: Instead of focusing on relationships between individual products, we study the relationships between their respective categories. For example, given that the spatula is related to the blender, a relationship can be established between “Kitchen Utensils” and “Small Appliances”.

5. Probability Calculation: Suppose, among 100 collections with the root category “kitchen”, “Kitchen Utensils” is mentioned in 90 collections. Among these collections, 80 also associate “Kitchen Utensils” with “Small Appliances”: $Prob_m(Kitchen ~Utensils, Small ~Appliances) = \frac{80}{90}$.

6. Important Condition: Suppose we also have more general categories such as “Indoor DIY” and “Outdoor DIY”. If a product from the “Indoor DIY” category has no match with a product from “Outdoor DIY”, then we would not calculate their co-occurrence probability because they do not belong to the same root category.

7. Using Transactional Data (Candidate Generator 2 - CG 2)

At this stage, we establish links between products based on purchase history.

To do this, we collect all online transactions where at least two products were purchased within a defined period, such as one year, for example.

Based on these transactions, we compile a list of all purchased products, designated $P_p={p_{p,1},…,p_{p,q}}$. We then construct a list of relationships between these products, denoted $R_p$ with $R_p = { rp(pp_i, pp_j), \ldots, rp(pp_k, pp_l) }$. A relationship $r_p(p_{p,i}, p_{p,j})$ means that products $p_{pR_p,i}$ and $p_{p,j}$ were purchased together in the same transaction. If two products are frequently bought together, this pair will appear multiple times in $R_p$.

Similarly to the previous section, for each product in $P_p$, we identify its category or hierarchy. Then, instead of focusing on relationships between individual products, we convert them into relationships between their respective hierarchies, generating a new set of relationships, designated by $Q_p$.

We conclude by calculating the probability. For hierarchies within the same general category, we evaluate the likelihood of them being co-purchased. This probability is derived by dividing the occurrence of this hierarchy relationship by the frequency of the hierarchy itself in $Q_p$.

Here is a concrete example:

1. Transaction Collection:

• We extract all transactions where at least two products were purchased together.
• After this extraction, we gather a list of products, including items such as: pans, spatulas, towels, faucets, sponges, soaps, etc. This list is designated by $P_m$.
• We repeat this process for each expert domain, such as “Kitchen” and “Bathroom”.

1. Product Hierarchy: Each product belongs to a specific category:
   • Kitchen Utensils: pans, spatulas
   • Small Appliances: blender, mixer
   • Bathroom Accessories: towels, soaps
   • Bathroom Fixtures: faucets
   • Cleaning Products: sponges
2. Relationships Between Products: Suppose, based on supplier information, we know that:

• The spatula and the pan have a relationship because they are often purchased together.

• We also know that the spatula has a relationship with small appliances because they are also bought together.

• Towels and soaps also have a relationship for the same reason.

  These relationships are our $R_m$.

1. Transformation into Hierarchy Relationships: Instead of focusing on relationships between individual products, we examine the relationships between their categories. Thus, since the spatula is related to the blender, we can establish a relationship between “Kitchen Utensils” and “Small Appliances”.
2. Probability Calculation: Suppose, among 100 purchases with the root category “kitchen”, 80 mention both “Kitchen Utensils” and “Small Appliances”, but “Kitchen Utensils” appears in 90 of these purchases: $Prob_m(Kitchen ~Utensils, Small ~Appliances) = \frac{80}{90}$.
3. Important Condition: For a general category like “Home Products”, we can also break down the probability of co-purchase between more specific categories, such as “Kitchen Utensils” and “Bathroom Accessories”, provided these products belong to the same general category.

Now that the probabilities between hierarchies are defined, we can move on to the step of using textual data related to the products.

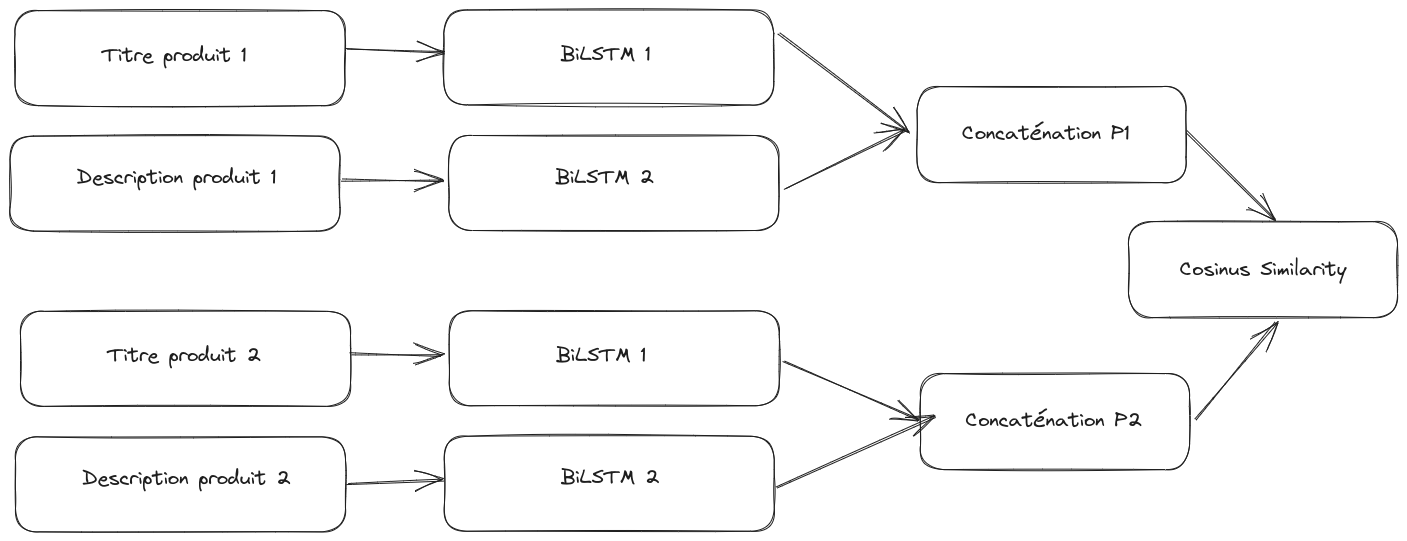
3. The Ranker - Using Text Embeddings

The objective of this part is to exploit the information present in the product’s title and description. The neural network used will allow representing the products in the form of embeddings. The constraint is as follows: two products will have close embeddings if they are considered to be part of the same collection.

To achieve this, a special neural network architecture, called “siamese biLSTM”, is used.

This architecture consists of two biLSTMs: one focuses on analyzing the product description while the other processes its title. After processing this information, the results obtained by these two biLSTMs are merged.

Siamese networks are trained to distinguish between two categories of product pairs: those belonging to the same collection and those from different collections. We chose not to use transactional data for this training because it is possible that two products bought simultaneously have no relation to each other (e.g., a barbecue and a drill).

To train the network, we rely on the knowledge of domain experts. When these experts believe that two products belong to the same series, we take this assertion as true. For each pair of products deemed similar or complementary by the experts, we also generate several pairs of products judged to be non-similar by randomly selecting other products from the database.

4. The Recommendation Process

Suppose we have a specific product, called the “anchor product.” For this product, there is a certain category or hierarchy.

1. Hierarchy Identification: For a given “anchor product”, identify its specific hierarchy or category.
2. Probability Calculation: Use one of the methods from sections 2.1 or 2.2 to evaluate the likelihood that the anchor product’s hierarchy is associated with other hierarchies within the same main category.
3. Selection of the Most Probable Hierarchies: Rank the probabilities from the previous step from highest to lowest, and retain the hierarchies with the highest probabilities.
4. Candidate Product Listing: For each high-probability hierarchy selected, list all associated products.
5. Embeddings Extraction: Use the siamese biLSTM architecture (or another relevant technique) to obtain a numerical representation of the anchor product and each product in the candidate set.
6. Color Matching Verification: Ensure that the anchor product’s color matches that of the candidate products. If so, calculate the similarity between the anchor product’s embeddings and those of the candidate products.
7. Final Set Creation: Rank the candidate products based on their similarity to the anchor product. Select the product(s) with the highest similarity for inclusion in the final set.

This process effectively filters candidate products based on their relevance to the anchor product, using both category information and embeddings to determine similarity.

Results

Three methods were studied by Home Depot. The first, called DomExp, uses supplier data. The second, named DomExpEmb, uses CG-1 and the text-based ranker. Finally, the third method employs CG-2 and the text-based ranker.

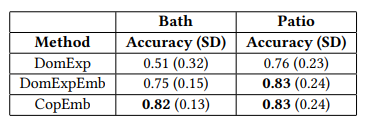
The best option is the approach coupling the candidate generator based on purchases and the ranker based on text embeddings. This is because suppliers often provide collections from the same brand. However, customers do not necessarily buy all products from the same brand. Therefore, there are more relevant relationships when based on transactional data.

Improvements

This paper presents a method based on 2019 technologies and is only version 1.0 of a recommendation engine based on product data and basket analysis at Home Depot. A more advanced version is presented here.

Here are two improvements to implement to advance the method:

• Ranker: Use a transformer-based architecture or fine-tune a BERT model on domain data.
• Ranker: Add image embeddings. The 2.0 version proposed by Home Depot incorporates this new type of information.