GCN with PyTorch for Co-Purchase Recommendation

Feb 22, 2026

Collaborative filtering captures what users like; Graph Convolutional Networks (GCN) capture how items relate to each other. When two products are frequently bought together, that co-purchase signal is an edge in a graph. A GCN trained on that graph learns item embeddings that encode neighbourhood structure — items in the same buying context end up geometrically close. This article explains how GCNs work, then walks through a complete PyTorch Geometric implementation for item-to-item recommendation.

1. How GCNs Propagate Information

A GCN stacks layers that each perform one round of message passing: every node aggregates the feature vectors of its neighbours, transforms them with a learned weight matrix, and applies a non-linearity. After $L$ layers, each node’s representation encodes information from its $L$-hop neighbourhood.

The propagation rule for layer $l$ is:

$$H^{(l+1)} = \sigma!\left(\hat{A},H^{(l)},W^{(l)}\right)$$

where:

$H^{(l)} \in \mathbb{R}^{n \times d}$ — node feature matrix at layer $l$
$W^{(l)}$ — trainable weight matrix
$\sigma$ — non-linear activation (ReLU)
$\hat{A} = \tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}$ — symmetrically normalised adjacency

$\tilde{A} = A + I$ adds self-loops so each node also retains its own features. $\tilde{D}$ is the diagonal degree matrix of $\tilde{A}$. The normalisation prevents the aggregated sum from growing with node degree.

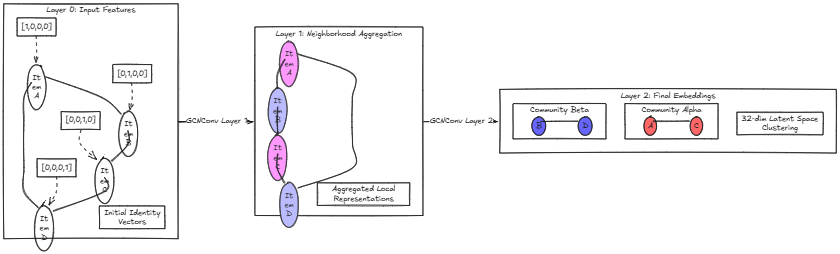gcn-message-passing Figure: Two rounds of message passing turn raw item features into neighbourhood-aware embeddings.

2. Co-Purchase Graph Construction

Nodes are items. An undirected edge $(i, j)$ exists when items $i$ and $j$ appear together in at least one transaction. Initial node features are one-hot identity vectors — a neutral starting point that lets the GCN learn all structure from the graph topology.

import torch
import numpy as np
from torch_geometric.data import Data

np.random.seed(42)
torch.manual_seed(42)

N_ITEMS = 20  # toy catalogue of 20 items

# Simulate co-purchases: items in the same "category" (0–6, 7–13, 14–19)
# are bought together with probability 0.7; cross-category with 0.05.
edges = []
for i in range(N_ITEMS):
    for j in range(i + 1, N_ITEMS):
        same_cat = (i // 7) == (j // 7)
        if np.random.random() < (0.7 if same_cat else 0.05):
            edges.extend([[i, j], [j, i]])  # undirected → both directions

edge_index = torch.tensor(edges, dtype=torch.long).t().contiguous()
x = torch.eye(N_ITEMS, dtype=torch.float)  # one-hot node features

data = Data(x=x, edge_index=edge_index, num_nodes=N_ITEMS)
print(f"Nodes: {data.num_nodes} | Edges: {data.num_edges}")

3. GCN Encoder

A two-layer GCN maps the $N \times N$ identity matrix to $N \times 32$ embeddings. The first layer expands into a hidden space; the second projects to the final embedding dimension.

import torch.nn as nn
import torch.nn.functional as F
from torch_geometric.nn import GCNConv

class GCNEncoder(nn.Module):
    def __init__(self, in_channels: int, hidden: int, out_channels: int):
        super().__init__()
        self.conv1 = GCNConv(in_channels, hidden)
        self.conv2 = GCNConv(hidden, out_channels)

    def forward(self, x, edge_index):
        x = F.relu(self.conv1(x, edge_index))
        x = F.dropout(x, p=0.3, training=self.training)  # regularise
        return self.conv2(x, edge_index)

model = GCNEncoder(in_channels=N_ITEMS, hidden=64, out_channels=32)

4. Training with Link Prediction

The task is link prediction: the model should score real co-purchase pairs higher than random pairs. For each training step, negative_sampling draws item pairs that share no edge. The objective is binary cross-entropy on dot-product scores.

from torch_geometric.utils import negative_sampling

optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

def bce_link_loss(z, pos_edge_index, neg_edge_index):
    pos_score = (z[pos_edge_index[0]] * z[pos_edge_index[1]]).sum(-1)
    neg_score = (z[neg_edge_index[0]] * z[neg_edge_index[1]]).sum(-1)
    scores = torch.cat([pos_score, neg_score])
    labels = torch.cat([
        torch.ones(pos_score.size(0)),
        torch.zeros(neg_score.size(0)),
    ])
    return F.binary_cross_entropy_with_logits(scores, labels)

model.train()
for epoch in range(1, 301):
    optimizer.zero_grad()
    z = model(data.x, data.edge_index)
    neg_edge = negative_sampling(
        edge_index=data.edge_index,
        num_nodes=N_ITEMS,
        num_neg_samples=data.edge_index.size(1),  # 1:1 positive/negative ratio
    )
    loss = bce_link_loss(z, data.edge_index, neg_edge)
    loss.backward()
    optimizer.step()
    if epoch % 100 == 0:
        print(f"Epoch {epoch:3d} | Loss: {loss.item():.4f}")

5. Generating Recommendations

After training, cosine similarity between embeddings drives recommendations. Known co-purchase neighbours are excluded to surface genuinely new suggestions.

model.eval()
with torch.no_grad():
    embeddings = model(data.x, data.edge_index)
    embeddings = F.normalize(embeddings, p=2, dim=-1)  # unit vectors → cosine = dot product

def recommend(item_id: int, embeddings, top_k: int = 5) -> list[int]:
    scores = embeddings @ embeddings[item_id]   # cosine similarity to all items
    scores[item_id] = -1                         # exclude self
    # Mask out existing co-purchase edges
    known = data.edge_index[1][data.edge_index[0] == item_id]
    scores[known] = -1
    return scores.topk(top_k).indices.tolist()

for anchor in [0, 7, 14]:
    recs = recommend(anchor, embeddings)
    print(f"Item {anchor:2d} → top-5 recommendations: {recs}")

Items 0, 7, and 14 are the respective category anchors. Correct recommendations should surface items from the same category (0–6, 7–13, 14–19).

Prerequisites

pip install torch torch_geometric numpy

PyTorch Geometric requires matching torch and CUDA versions. Follow the official installation guide if the default install fails.

Conclusion

A two-layer GCN turns a co-purchase graph into item embeddings that reflect buying context. The link prediction objective requires no user data — only item-item co-occurrence signals. This makes it a strong baseline for cold-start scenarios where user histories are sparse.

Directions for improvement:

Richer node features: replace one-hot identity with product text embeddings (e.g., from a sentence transformer) to benefit categories with few co-purchase edges.
LightGCN: remove activation functions and weight matrices entirely — the LightGCN paper shows this simplification improves recommendation quality by reducing overfitting.
Temporal edges: weight edges by recency to discount old purchasing patterns.

For a different graph embedding approach applied to the same recommendation problem, see the article on Cleora graph embeddings.